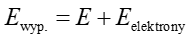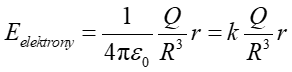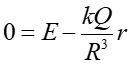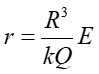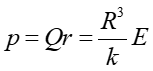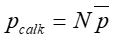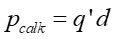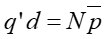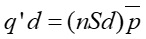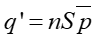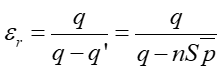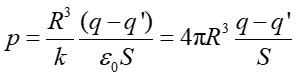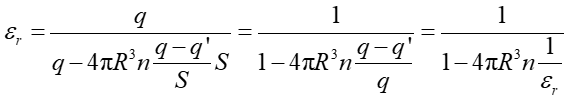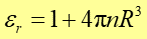Dielektryk w polu elektrycznym - rozważania ilościowe
Rozpatrzmy atom umieszczony w zewnętrznym polu elektrycznym o natężeniu E. Wówczas na atom działa siła, która przesuwa chmurę elektronową o r względem jądra atomowego (rysunek 1).
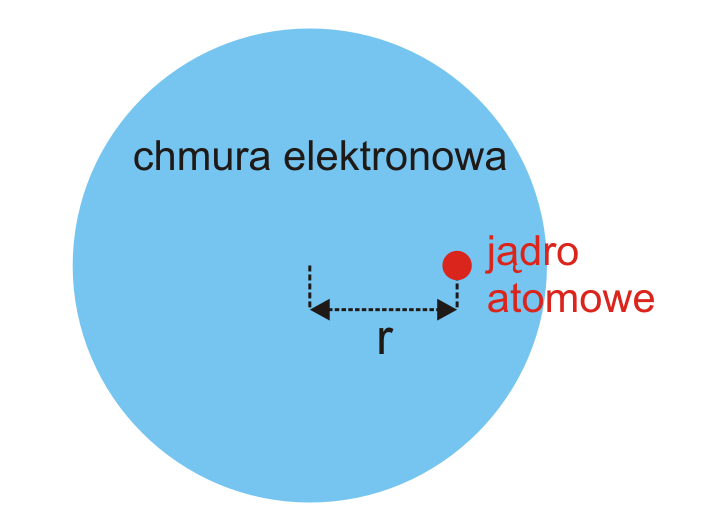
Rys. 1. Sferyczna chmura elektronowa przesunięta zewnętrznym polem elektrycznym względem jądra atomu na odległość r
Wówczas atom ma indukowany moment dipolowy p, a wypadkowe pole elektryczne w miejscu jądra jest sumą pola zewnętrznego i pola od chmury elektronowej
|
(1) |
Jeżeli potraktujemy, w naszym uproszczonym modelu, chmurę elektronową jako jednorodnie naładowaną kulę o promieniu R to pole elektryczne wytworzone przez chmurę elektronową w odległości r (r < R) od jej środka jest dane wzorem (18.17)
|
(2) |
Ponieważ jądro znajduje się w położeniu równowagi (nie przemieszcza się) więc Ewyp. = 0, skąd dostajemy
|
(3) |
|
(4) |
Zatem, indukowany moment dipolowy jest równy
|
(5) |
Moment p zgodnie z oczekiwaniami jest proporcjonalny do natężenia zewnętrznego pola elektrycznego E.
Rozpatrzmy teraz dielektryk, w którym znajduje się N atomów (cząsteczek). Jeżeli każdy
atom ma średni moment dipolowy ![]() skierowany zgodnie
z zewnętrznym polem E to całkowity moment dipolowy
skierowany zgodnie
z zewnętrznym polem E to całkowity moment dipolowy
|
(6) |
Z drugiej strony indukowany ładunek q' pojawia się jedynie na powierzchni dielektryka więc dla kondensatora płaskiego, wypełnionego dielektrykiem, którego okładki o powierzchni S są umieszczone w odległości d
|
(7) |
Łącząc te wyrażenia otrzymujemy
|
(8) |
|
(9) |
gdzie n koncentracją atomów (cząsteczek) tj. ilością atomów w jednostce objętości n = N/(Sd). Ostatecznie więc
|
(10) |
Podstawiamy tę wielkość do wzoru na εr
|
(11) |
Pokazaliśmy powyżej, że indukowany moment dipolowy p wynosi 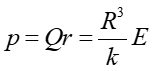 .
Podstawiając do tego wzoru wyrażenie na natężenie pola elektrycznego w kondensatorze płaskim (wzór 20.14)
otrzymujemy
.
Podstawiając do tego wzoru wyrażenie na natężenie pola elektrycznego w kondensatorze płaskim (wzór 20.14)
otrzymujemy
|
(12) |
Wstawiając to wyrażenie do wzoru (11) obliczamy εr
|
(13) |
|
(14) |
Otrzymana zależność jest przybliżona ze względu na znaczne uproszczenia przyjętego modelu atomu jednak pokazuje, że przenikalność dielektryczna εr jest większa od jedności i że zależy od właściwości dielektryka takich jak koncentracja atomów n i promień atomu R.


 Kondensator z dielektrykiem
Kondensator z dielektrykiem