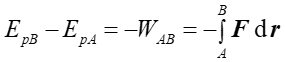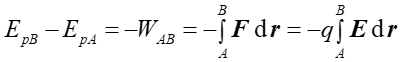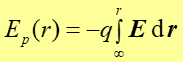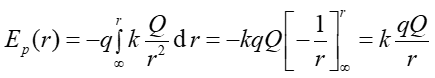19.1 Energia potencjalna w polu elektrycznym
Zgodnie z naszymi rozważaniami w rozdziale 8.2 (moduł II), różnica energii potencjalnej Ep pomiędzy punktami A i B jest równa pracy (ze znakiem minus) wykonanej przez siłę zachowawczą przy przemieszczaniu ciała od A do B i wynosi
|
(19.1) |
Dla pola elektrycznego energia potencjalna wynosi
|
(19.2) |
gdzie E jest natężeniem pola elektrycznego. Siły elektryczne są siłami zachowawczymi i wartość pracy nie zależy od wyboru drogi pomiędzy punktami A i B. Jeżeli teraz podobnie jak dla grawitacyjnej energii potencjalnej przyjmiemy, że energia potencjalna pola elektrycznego jest równa zeru w nieskończoności to wówczas energia potencjalna w danym punkcie r pola elektrycznego jest dana wyrażeniem
|
(19.3) |
Jeżeli źródłem pola elektrycznego jest ładunek punktowy Q to energia potencjalna w odległości r od niego jest równa
|
(19.4) |
Zauważmy, że energia potencjalna ładunku w polu elektrycznym zależy wielkości tego ładunku.


 Przykłady zastosowania prawa Gaussa II
Przykłady zastosowania prawa Gaussa II