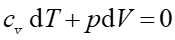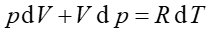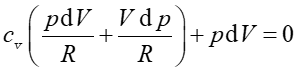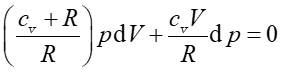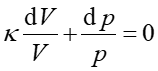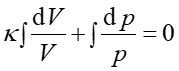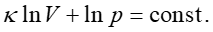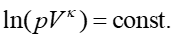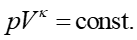Równanie Poissona dla przemiany adiabatycznej
W przemianie adiabatycznej nie zachodzi wymiana ciepła z otoczeniem. Oznacza to, że dQ = 0 i pierwsza zasada termodynamiki przyjmuje postać dU + pdV = 0. Równanie to możemy przepisać w postaci
|
(1) |
Różniczkując równanie stanu gazu doskonałego (15.15) otrzymujemy (dla jednego mola gazu)
|
(2) |
Łącząc oba powyższe równania (eliminując dT) otrzymujemy
|
(3) |
|
(4) |
Podstawiając 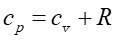 otrzymujemy
otrzymujemy
|
(5) |
gdzie ![]() . Możemy teraz scałkować to równanie
. Możemy teraz scałkować to równanie
|
(6) |
|
(7) |
Zapisując inaczej otrzymany wynik
|
(8) |
|
(9) |


 Rozprężanie izotermiczne i adiabatyczne
Rozprężanie izotermiczne i adiabatyczne