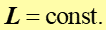11.2 Dynamika ruchu obrotowego
Jak wynika z naszego codziennego doświadczenia w ruchu
obrotowym ważna jest nie tylko wartość siły, ale to gdzie i pod jakim kątem
jest ona przyłożona. Na przykład, drzwi najłatwiej jest otworzyć przykładając
siłę na ich zewnętrznej krawędzi i pod kątem prostym do płaszczyzny
drzwi. Siła przyłożona wzdłuż płaszczyzny drzwi jak i siła przyłożona
w miejscu zawiasów nie pozwalają na ich obrót.
Dla ruchu obrotowego wielkością, która odgrywa rolę
analogiczną do siły w ruchu postępowym jest moment
siły ![]() (tzw. moment obrotowy) τ. Jeżeli siła F jest przyłożona w
pewnym punkcie to moment siły τ
względem tego punktu jest definiowany jako
(tzw. moment obrotowy) τ. Jeżeli siła F jest przyłożona w
pewnym punkcie to moment siły τ
względem tego punktu jest definiowany jako
|
Definicja |
|
(11.5) |
gdzie wektor r reprezentuje położenie punktu względem wybranego inercjalnego układu odniesienia.
Moment siły jest wielkością wektorową, której wartość bezwzględna wynosi (iloczyn wektorowy)
|
(11.6) |
Wielkość r nazywamy ramieniem siły ![]() .
Z równania (11.6) wynika, że tylko składowa siły prostopadła do ramienia
.
Z równania (11.6) wynika, że tylko składowa siły prostopadła do ramienia ![]() wpływa na moment siły.
wpływa na moment siły.
Moment pędu
Zdefiniujmy teraz wielkość, która w ruchu obrotowym odgrywa rolę
analogiczną do pędu. Wielkość L nazywamy momentem
pędu ![]() i definiujemy jako
i definiujemy jako
|
Definicja |
|
(11.7) |
gdzie p jest pędem punktu materialnego, a r reprezentuje jego położenie względem wybranego inercjalnego układu odniesienia. Wartość L wynosi
|
(11.8) |
Istnieje bezpośrednia zależność pomiędzy momentem siły i momentem pędu. Żeby ją wyprowadzić zróżniczkujmy obie strony równania (11.7)
|
(11.9) |
Ponieważ wektory v oraz p są równoległe to ich iloczyn wektorowy jest równy zeru. Natomiast drugi składnik równania jest zgodnie z definicją (11.5) wypadkowym momentem siły. Otrzymujemy więc
|
(11.10) |
|
Prawo, zasada, twierdzenie Wypadkowy moment siły działający na punkt materialny jest równy prędkości zmian momentu pędu. |
To jest sformułowanie drugiej zasadę dynamiki ruchu obrotowego. Równanie (11.10) jest analogiczne do równania (4.6) dla ruchu postępowego. Analogicznie możemy sformułować pierwszą zasadę dynamiki ruchu obrotowego
|
Prawo, zasada, twierdzenie Ciało sztywne, na które nie działa moment siły pozostaje w spoczynku lub porusza się ruchem obrotowym jednostajnym. |
oraz trzecią zasadę dynamiki ruchu obrotowego
|
Prawo, zasada, twierdzenie Jeżeli dwa ciała oddziałują wzajemnie, to moment siła z jakim działa ciało drugie na ciało pierwsze jest równy i przeciwnie skierowany do momentu siły, z jakim ciało pierwsze działa na drugie. |
Zachowanie momentu pędu
Dla układu n cząstek możemy zsumować momenty sił działające na poszczególne punkty materialne
|
(11.11) |
gdzie L oznacza teraz całkowity moment pędu układu. Zauważmy, że
|
Prawo, zasada, twierdzenie Jeżeli na układ nie działa zewnętrzny moment siły (lub wypadkowy moment sił zewnętrznych jest równy zeru) to całkowity moment pędu układu pozostaje stały. |
Zależność powyższa wyraża zasadę zachowania momentu pędu.
|
(11.12) |
|
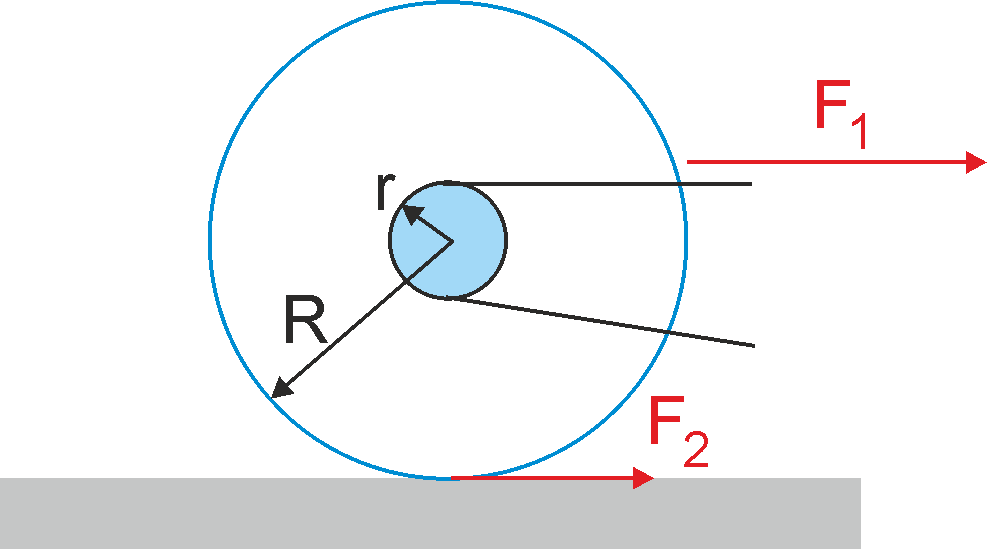
Ćwiczenie Rozpatrzmy teraz następujący przykład. Rower jedzie ze stałą prędkością gdy siła działająca pomiędzy nawierzchnią i kołem F2 = 5 N. Z jaką siłą F1 łańcuch ciągnie zębatkę jeżeli stosunek R/r = 10? Sprawdź obliczenia i wynik. |
|


 Kinematyka ruchu obrotowego
Kinematyka ruchu obrotowego
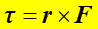
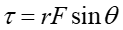
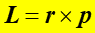
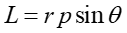
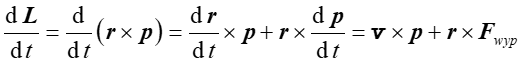
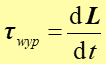

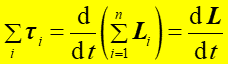
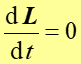 lub
lub