Algorytmy heurystyczne i funkcje testowe

Człowiek wymyślił różne algorytmy heurystyczne (przeważnie inspirowane przyrodą), których zadaniem jest optymalizacja. Sprowadza się to do znajdywania ekstremów globalnych zagadnień sprowadzonych do postaci funkcji. Każdy taki algorytm wymaga walidacji, a robi się to za pomocą tzw. funkcji testowych, czyli funkcji o skomplikowanych przebiegach i licznych pułapkach, przeważnie w postaci ekstremów lokalnych.

Na poniższej animacji przedstawiono algorytm roju cząstek testowany na funkcji Rosenbrock typu Valley w zakresie (-10 10). Jest to funkcja o pozornie prostym przebiegu, jednak jej trudność polega na bardzo niskich gradientach w okolicach ekstremum globalnego f(x,y)=0 w punkcie (1,1). Pomimo tego, algorytm poradził sobie z tą funkcją bez większych problemów.

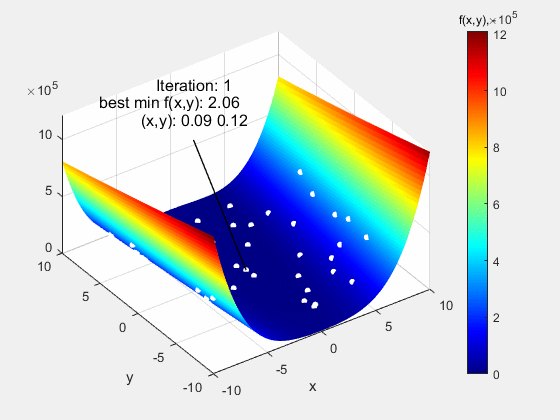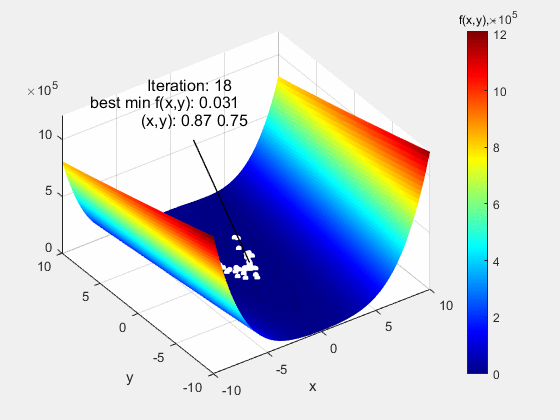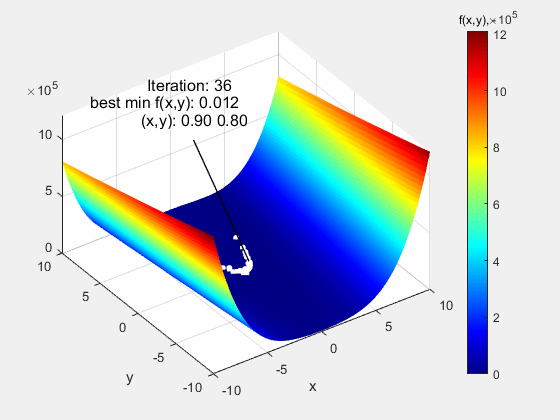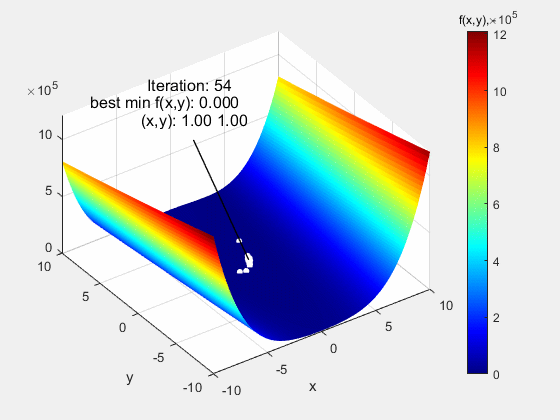
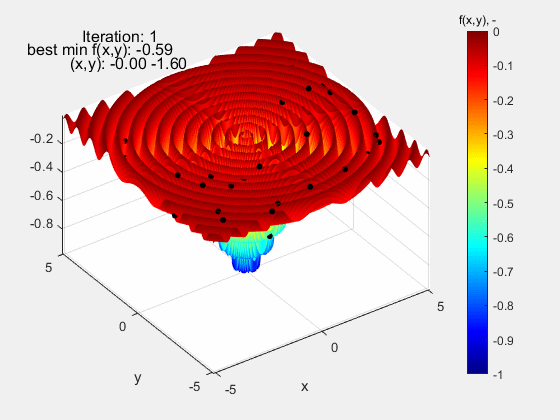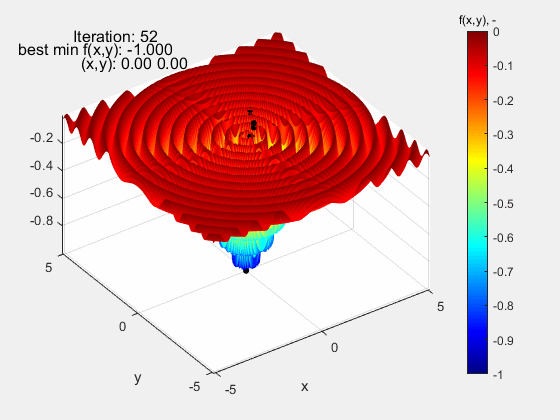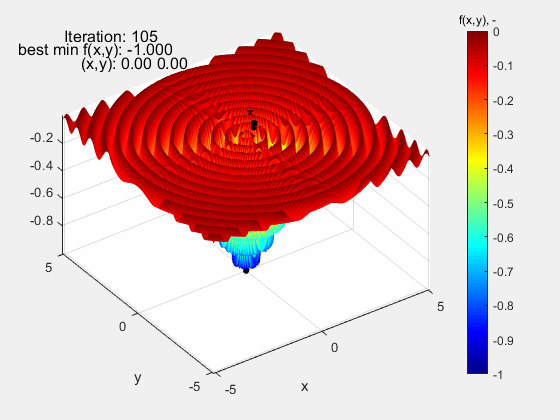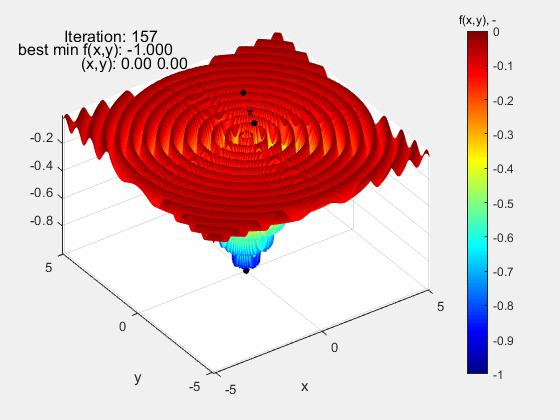
Następną funkcją testową, na której sprawdzany był algorytm roju cząstek, była funkcja Dropwave w zakresie (-5.12 5.12). Jest to bardzo wymagająca funkcja z uwagi na liczne ekstrema lokalne (charakterystyczne pofałdowanie) o rosnącej amplitudzie w miarę zbliżania się do ekstremum globalnego f(x,y)=-1 w punkcie (0,0). Również i w tym przypadku algorytm nieźle sobie poradził.

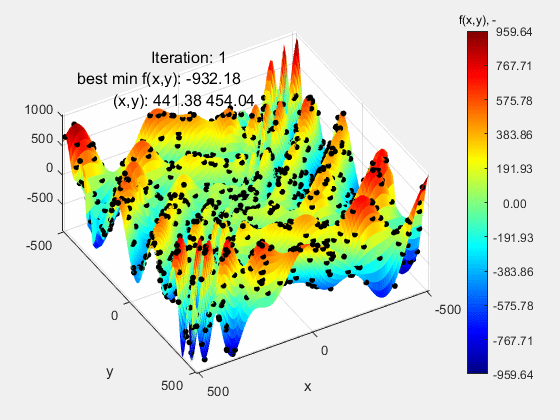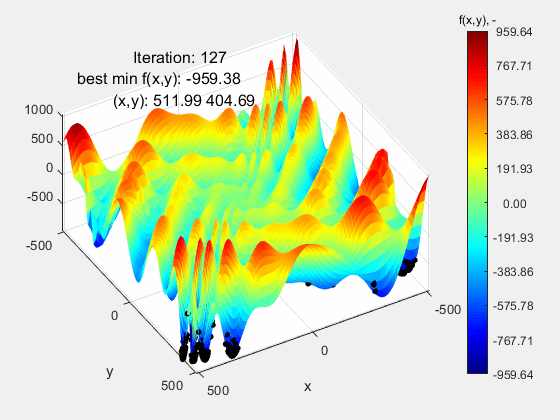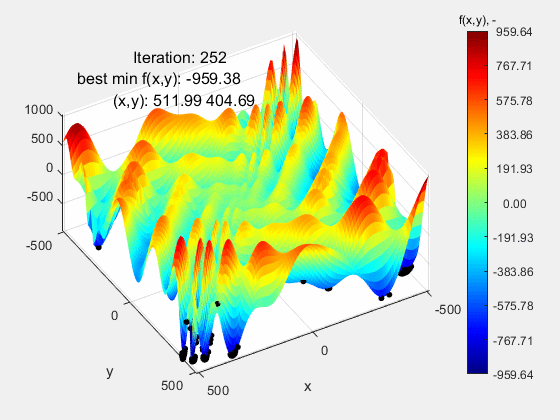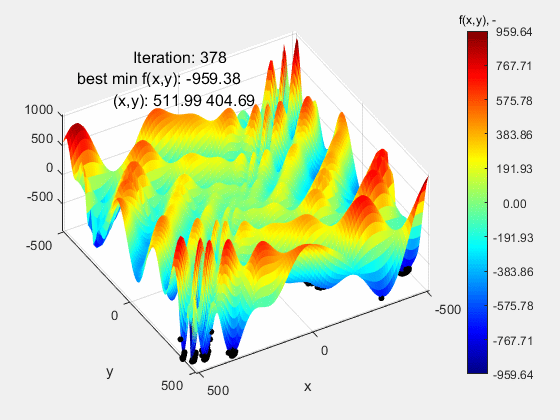
Najbardziej wymagającą funkcją testową okazała się funkcja Eggholder, której przebieg może nie sprawiać wrażenia „trudnego”. Nic bardziej mylnego. Jej trudność leży w dwóch rzeczach: 1 – bardzo szeroki zakres mieszczący się w przedziale (-512 512) oraz peryferyjnie zlokalizowane ekstremum globalne f(x,y)=-959.64 w punkcie (512, 404), a więc opierające się o górny zakres funkcji. Dla zwiększenia poziomu trudności, ekstremum lokalne porównywalne z globalnym znajduje się względnie daleko od niego, co dodatkowo „myli” algorytm. Jak widać, algorytm nie poradził sobie z tą funkcją kończąc niedaleko ekstremum globalnego f(x,y)=-959.38 w punkcie (511.99 404.69). Powodzenia z tą funkcją!

Wszystkie zaprezentowane funkcje testowe znaleźć można tutaj.