Heuristic algorithms and test functions

A various heuristic algorithms have been developed (mostly inspired by the nature), the task of which is optimization. It comes down to finding the global extremes of problems reduced to the form of functions. Each algorithm requires validation, and here the so-called test functions come in help, i.e. complex functions with numerous traps, usually in the form of local extremes.

The animation below shows the particle swarm algorithm tested on the function Rosenbrock of type Valley in the range of (-10 10). It is a function with an apparently simple course, but its difficulty lies in very low gradients around the global extreme f (x, y) = 0 at the point (1,1). Despite this, the algorithm coped with this function without any major problems.

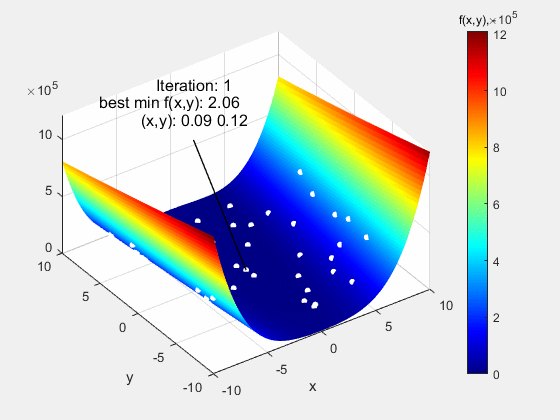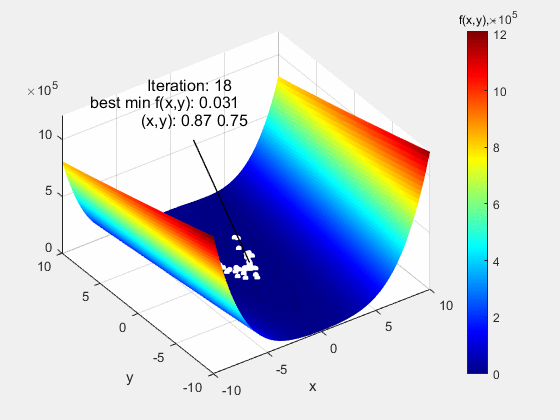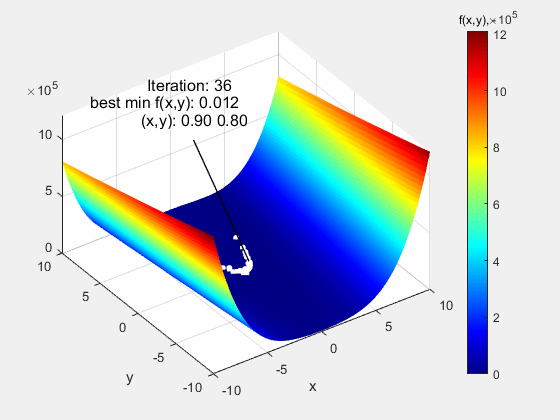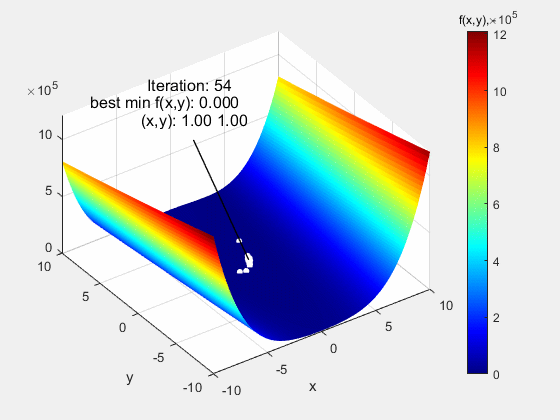
The particle swarm algorithm was also tested on function Dropwave in the range (-5.12 5.12). It is a very demanding function due to numerous local extremes (characteristic folding) of increasing amplitude as the global extremum f (x, y) = - 1 at the point (0,0) is approached. Also in this case, the algorithm did quite well.

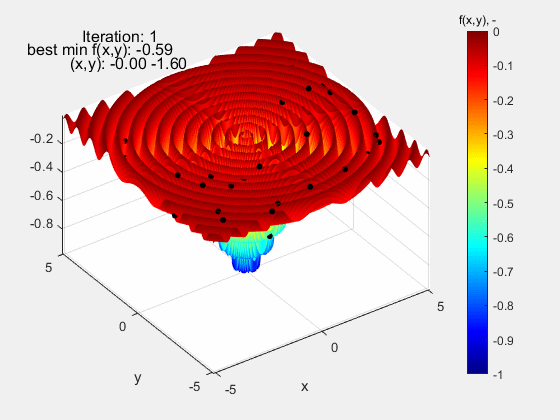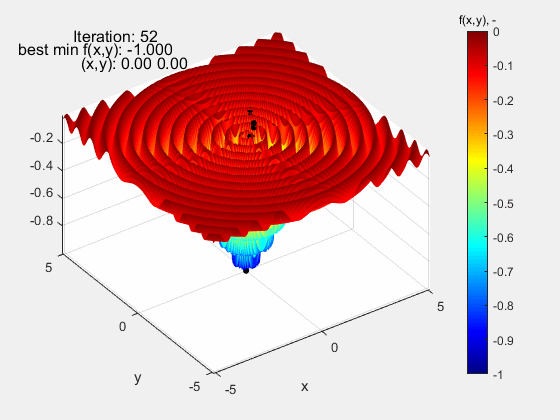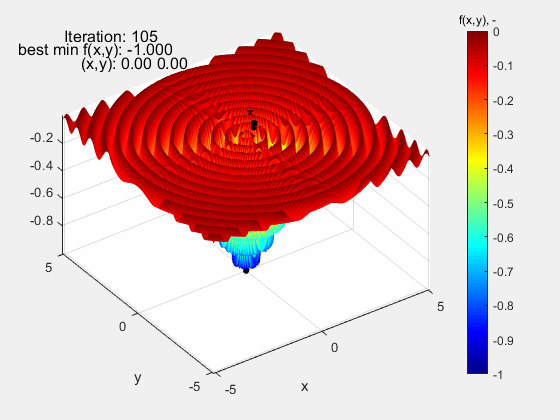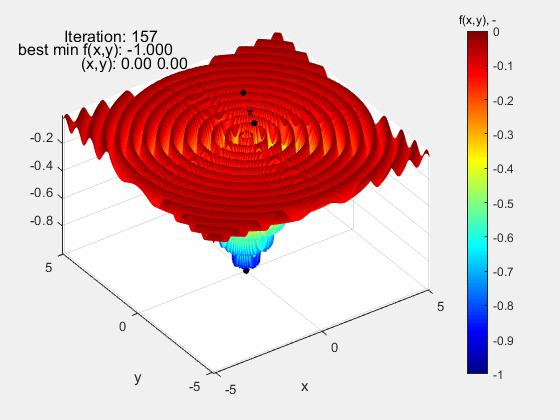
The Eggholder function turned out to be the most demanding test function. Eggholder, której przebieg może nie sprawiać wrażenia „trudnego”. Nic bardziej mylnego. Jej trudność leży w dwóch rzeczach: 1 – bardzo szeroki zakres mieszczący się w przedziale (-512 512) oraz peryferyjnie zlokalizowane ekstremum globalne f(x,y)=-959.64 w punkcie (512, 404), a więc opierające się o górny zakres funkcji. Dla zwiększenia poziomu trudności, ekstremum lokalne porównywalne z globalnym znajduje się względnie daleko od niego, co dodatkowo „myli” algorytm. Jak widać, algorytm nie poradził sobie z tą funkcją kończąc niedaleko ekstremum globalnego f(x,y)=-959.38 w punkcie (511.99 404.69). Powodzenia z tą funkcją!

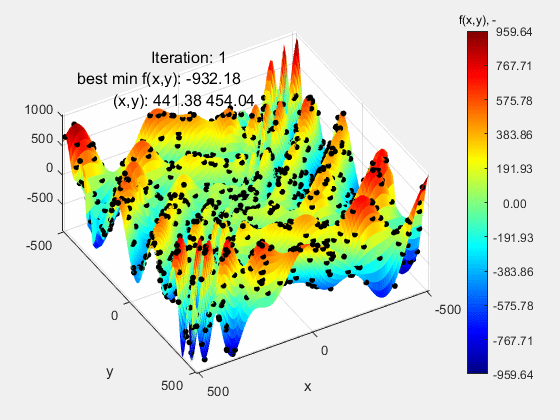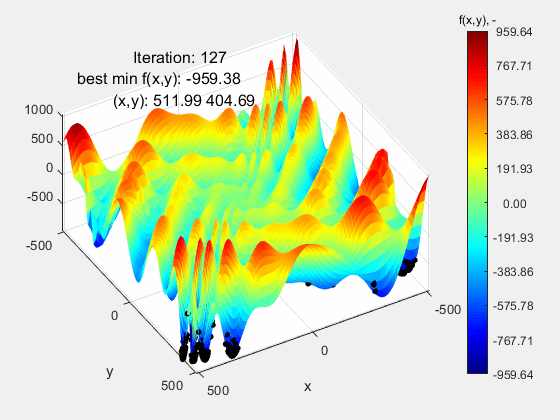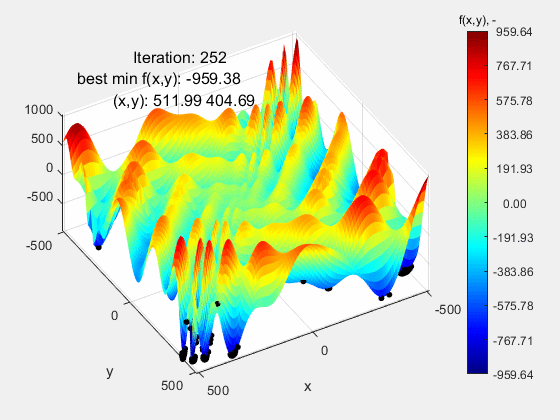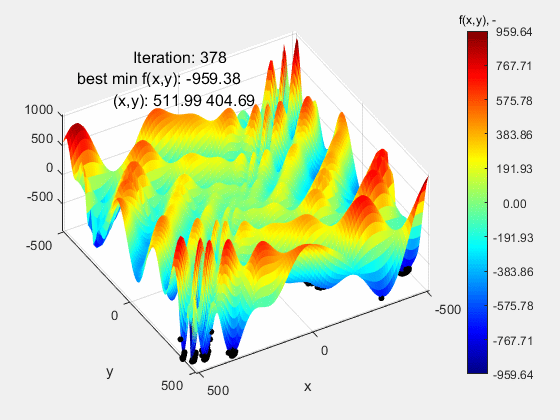
All the presented test functions can be found here.