FEM

The Finite Element Method (FEM) is a widely used tool in numerical calculations consisting in the specific discretization of the computational domain in the so-called finite elements using the local coordinate system, simple polynomial functions and the Jacobi matrix. This method allows you to transform distorted finite elements into simple, equal and regular equivalents, simplifying calculations at the same time. Initially used in mechanics, it quickly found application in other areas, including in heat flow.

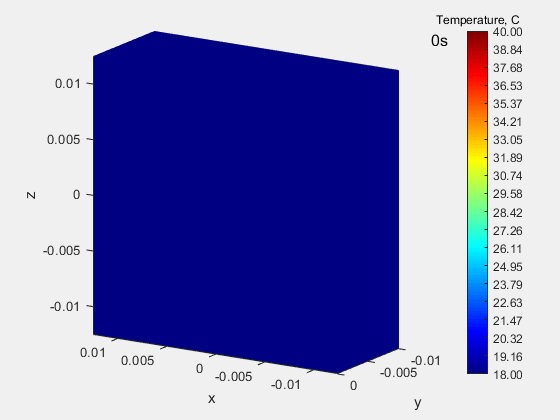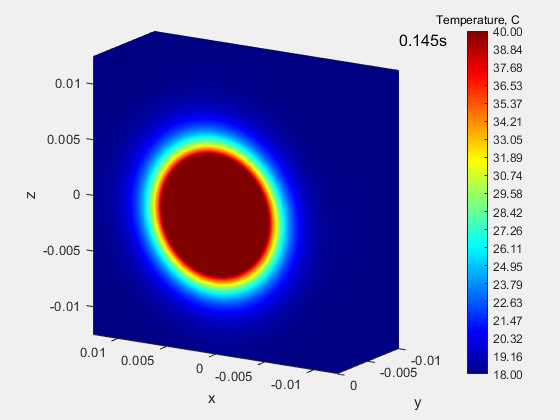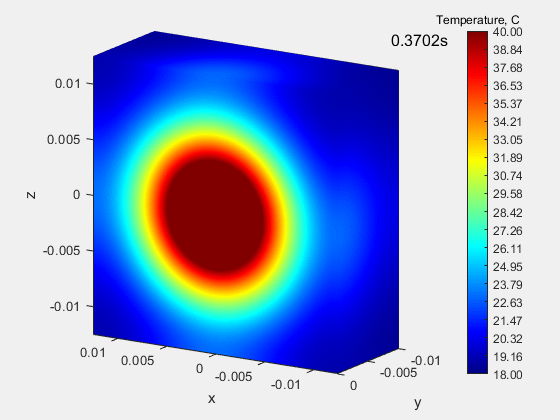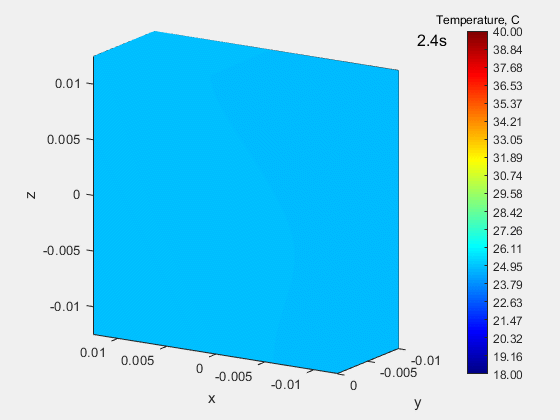
The animation below shows the process of heating a block made of isotropic material with a constant and equal in all directions the thermal conductivity coefficient k, equal to 55.5 W / (m K). The so-called Type II boundary condition (Neumann condition), which consists in assigning a specific heat flux to a given surface. Here, the heat flux is applied for 0.19 seconds to a small circular area. The material is isotropic, so heat spreads uniformly in all directions, so isotherms keep the shape of a circle.

In the following case, the same heat flux is also given for 0.19 s over a small circular area, with the difference that the block material is orthotropic, i.e. the heat conduction coefficient depends on the direction and amounts to k = (55.5 10.5 10.5) for the x, y and z components, respectively. The x component is about 5 times larger than the other components, so the heat in the x direction flows faster, thus creating a characteristic ellipse.

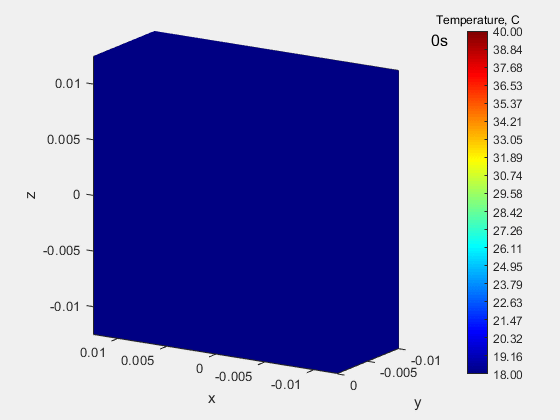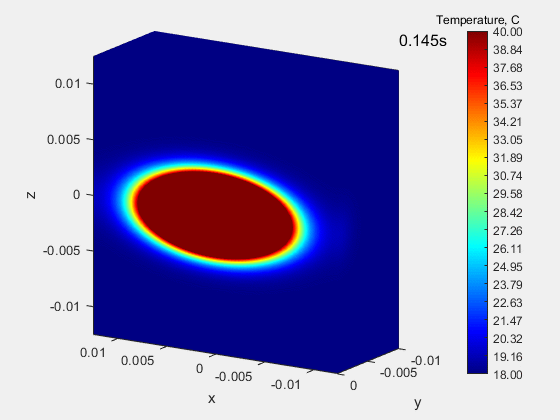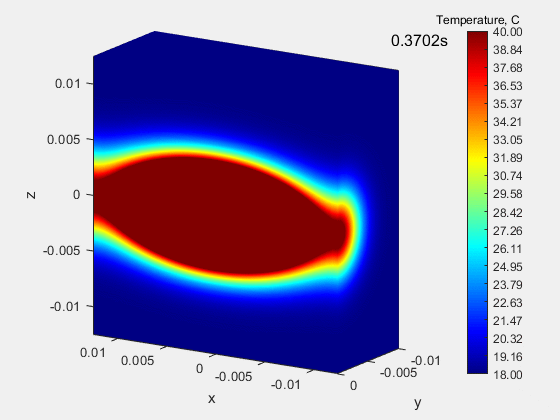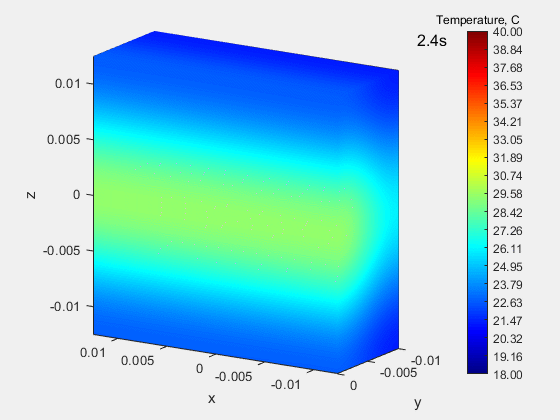
Strumień ciepła w przypadku tej analizy symuluje plamkę lasera w badaniach przewodności cieplnej metodą Parkera.