::Genetic Algorithm::

    The way genetic algorithms work is not accidentally similar to the phenomenon of biological evolution, since it is biology where the creator of the algorithms John Henry Holland found his inspiration.

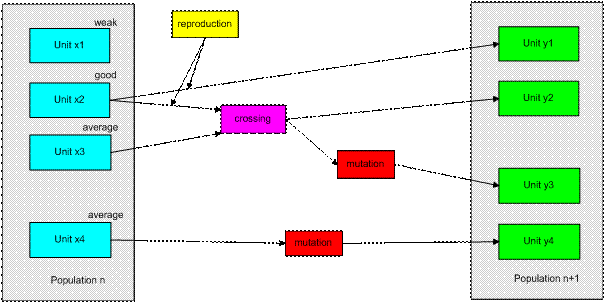
Genetic algorithm works on population of units:

where: n is the number of the population, whereas R stands for its size.

Genetic algorithms in their classic form do not in any way use the knowledge on the the problem solved. It is the fact that the better units from the previuos generation get to every next population, and that genetic operators exchange information included in the units,thus creating new, potantially better solutions, that the algorithms find the solutions. The process of creating of a new population is depicted below.

    ::A bit of history::

1957-62: Barricelli, Fraser, Martin, Cockerham – modelling genetic processes

1960: Holland ( University of Michigan)

- systems of adaptation / adaptative systems -> Genetic Algorithms

1967: Bagley – six- pawn game programme

1971: Hollstien;

1975: De Jong –function optimization

1985: Goldberg – gas pipeline work optimization

    ::The Poles, and genetic algorithms::

Michalewicz ( University of North Carolina, Charlotte, USA)

‘Genetic algorithms + data structures = evolution programmes’

Buller (ATR, Kioto, Japan) Sztuczny mózg. To już nie fantazje”

M. J. Kasperski, „Sztuczna Inteligencja. Droga do myœlšcych maszyn”

    ::Examples and application::

    Genetic algorithms are used to solve problems connected with optimalization, recognizing images, predicting movements on the stock exchange, creating computer graphic as well as projects of buildings and machines.

    ::Basic statements::

• Chromosome – it’s for example a string of bits. Every bit is representing single “gene” for example Women Man
• Recombination (or crossover) – it’s random operation witch cuts two of chromosomes which are recombinating in the same point and switch the parts of cut chromosomes. It’s important that “kids” are taking parents place.

11010010

    ↓↑    - recombination

00100101

      ↓↓   -Two New chromosomes:

11010101

00100010

• Mutating – inverting one or more random bit.

    ↓   - mutation

10010111

10110111 – chromosome after mutation.

• Selection to crossover is random
• Roulette weel method  - which are selecting the probability of choosing every chromosome. The method is based on one function.
• Line rank – this method is almost similar than the above but the function is different to every chromosome
• Tournament – much different than the other two methods, it’s based on random selection from all the population few chromosomes and from this group selected is the most valuable unit. The all tournament is needed to be repeated until new population is made.

ˇ        Population – has constant size, in every cycles of evolution all chromosomes are replaced by new ones.

ˇ        Solution of the problem is the most valuable unit (chromosome) at the last population. We have to set the end of evolution process. (For example the unit which has satisfying parameters)

    ::Travelling Salesman Problem::

In the Travelling Salesman Problem, the goal is to find the shortest distance between N different cities.

Testing every possibility for an N city tour would be N! math additions. A 30 city tour would be 2.65 X 1032 additions. Assuming 1 billion additions per second, this would take over 8,000,000,000,000,000 years. Adding one more city would cause the number of additions to increase by a factor of 31. Obviously, this is an impossible solution.

A genetic algorithm can be used to find a solution is much less time. Although it probably will not find the best solution, it can find a near perfect solution in less than a minute. There are two basic steps to solving the travelling salesman problem using a GA. First, create a group of many random tours in what is called a population. These tours are stored as a sequence of numbers. Second, pick 2 of the better (shorter) tours parents in the population and combine them, to create 2 new solutions children in the hope that they create an even better solution.

The idea of Genetic Algorithms is to simulate the way nature uses evolution. The good solutions reproduce to form new and hopefully better solutions in the population, while the bad solutions are removed.

The difficulty in the TSP using a GA is encoding the solutions. The encoding cannot simply be the list of cities in the order they are travelled. As shown below, the crossover operation will not work. The crossover point is the 3rd number

As you can see, the city 1 is used twice and city 5 is missing in child 1. A more complicated form of encoding (or a more complicated crossover) must be used. For example a matrix NxN where places according to connections between cites i shown as one bit 0 or 1.