Decision making - threshold voltage matching

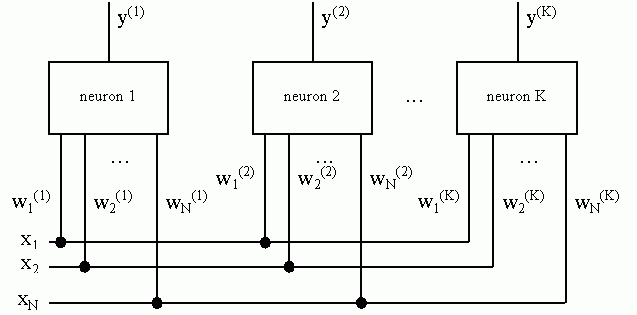
::Notice !!! All calculations are based on assumption that vectors are normalised.:: The simplest neural network consists of one layer of neurons, which inputs are connected to each other, Fig. 1. Such network might recognise as much different input vectors (e.g. characters) as the number of common neural cells is. It is possible when all neurons have distinct synaptic weights. Fig. 1. Layer of neurons K - number of neurons, N - number of neuron inputs. When the input signal appears X = [x₁; ...; x_n; ...; x_N], every neuron generates response y⁽¹⁾, ..., y^(k), y^(K). Thus, each output signal has to be compared with others. The simplest method of doing such comparison consists in usage of separate threshold functions (Fig. 2.) but these threshold values have to be set properly. 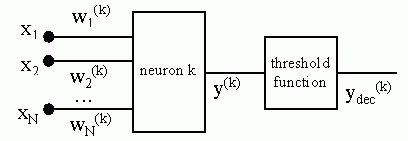Fig. 2. Neuron with threshold function Let's consider one-layer network that consists of two two-input neurons, Fig. 3. Fig. 3. One-layer network: two two-input neurons Let first neuron recognises input vector X = A = [a₁; a₂], and second neuron recognises input vector X = B = [b₁; b₂]. Then such equations are satisfied: w₁⁽¹⁾ = a₁ w₂⁽¹⁾ = a₂ w₁⁽²⁾ = b₁ w₂⁽²⁾ = b₂ For X = A the following responses are obtained: y⁽¹⁾ = w₁⁽¹⁾a₁ + w₂⁽¹⁾a₂ = a₁a₁ + a₂a₂ = 1 y⁽²⁾ = w₁⁽²⁾a₁ + w₂⁽²⁾a₂ = b₁a₁ + b₂a₂ = cos(γ) and for X = B: y⁽¹⁾ = w₁⁽¹⁾b₁ + w₂⁽¹⁾b₂ = a₁b₁ + a₂b₂ = cos(γ) y⁽²⁾ = w₁⁽²⁾b₁ + w₂⁽²⁾b₂ = b₁b₁ + b₂b₂ = 1 where γ - angle between A and B vectors. The attained results show that the response of the first neuron to vector B equals the response of the second neuron to vector A. The response of each neuron to "its" vector obviously equals 1. The threshold value may be set us arithmetic average of these answers: th = (1+cos(γ))/2 For instance, the responses to vectors A = [0; 1] and B = [1; 0] (Fig. 4) are: 1 and 0 (vectors are perpendicular) The threshold value can be set as 0,5. 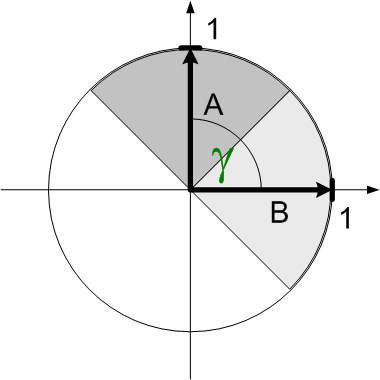Fig. 4. Taking into account greater number of neurons and vectros recognised by network the threshold value ought to equals the largest value computed for considered neuron. Naturally the greatest values are obtained for "the most similar" vectors. The angle between such vectors has the smallest value. Example. Vectors: A = [0; 1], B = [0,707; 0,707] and C = [0; -1], Fig. 5. 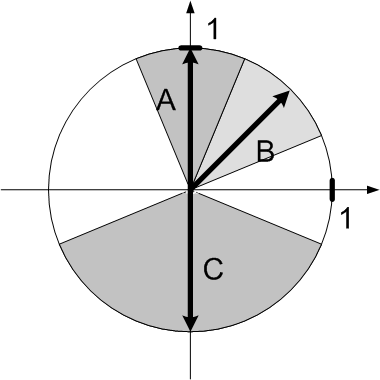Fig. 5. For each pair of vectors: for vector A: th_AB = 0,854 th_AC = 0 thus th_A = 0,854 for vector B: th_BA = 0,854 th_BC = 0.146 thus th_B = 0,854 for vector C: th_CA = 0 th_CB = 0,146 thus th_C = 0,146 References Ryszard Tadeusiewcz "Sieci neuronowe", Kraków 1992 Adnrzej Kos, Wykład "Przemysłowe zastosowania sztucznej inteligencji", 2003/2004

Łukasz Sanocki (2003/2004) mgr inż. Adam Gołda (2005) Katedra Elektroniki AGH
Last modified: 06.09.2004 Webmaster