::Theoretical preface::

     Neuron is a basic element of the neural network. The main feature of the single neuron is that it has many inputs and only one output. From the mathematical point of view neuron is an element that realizes function:

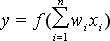
where f() is the activation function, w_i weights for all inputs, x_i neuron input values. Neuron is summing all elements of the input vector multiplied by the weights, and the result is used as the argument of the activation function, this way the neuron output value is created. In most of applications neuron inputs and weights are normalized. In geometry it is equal to move of input vector points to the surface of N dimensional sphere with unitary radius, where N is a size of the input vector. In the simplest case, for the two dimensional vector, normalization is the movement of all input points to the edge of the unitary radius circle. Normalization could be written as:

where x_i coordinate to normalize, x_j all of vector coordinates. Use of normalization either to input vectors or input weights of the neuron, improves learning neuron properties. We can use linear or nonlinear function, as an activation function. In the event of linear neuron, its mathematical equation could be written as follows:

It is one of the simplest of the neuron models, which is only occasionally used in practice because the most of phenomena in the surrounding world have nonlinear characteristics. As the example we can mean the biological neurons. Neuron could be biased; it means that it has additional input with constant value. The weight of that input is modified during the learning process like the other neuron weights. Generally we assume the bias input equal to one, in this case the neuron mathematical equation could be written as follows:

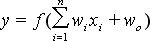
where f() is the activation function, w_i weights of all inputs, x_i neuron input values and w₀ is the weight value of the bias. When we assume that the bias input value is zero we obtain equation for non biased neuron. Now we should say what is the use of that “bias”.

    ::One dimensional case::

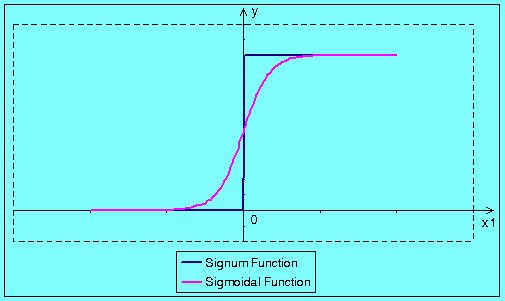
      The simplest way to describe the function of bias is to present it’s graphical interpretation for single input neuron with two activation functions. This interpretation is shown in the figure below.

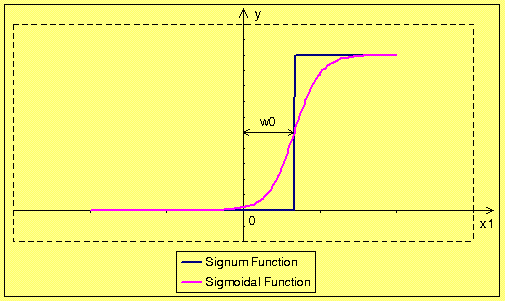
In these two figures we can see that the bias enables moving the activation threshold along the x-axis. When the bias is negative the movement is made to the right side, and when the bias is positive it the movement is made to the left side. Conclusion is that the biased neuron should learn even such input vectors that non biased neuron is not able to learn. We come to the conclusion that the additional weight cost us more calculations but it improves neuron properties. Normalization does not have any sense for single input neuron, because every normalized point could have only three different values –1, 0 or 1. Lets see normalization for biased single dimensional neuron. Realization of normalization of input vectors (the bias is the input equal to 1) and weights cause movement of all points to the edge of the circle with unitary radius. Result of that operation is shown in the figure below.

According to the sign of bias normalization all points are moved to the adequate part of the circle, for positive bias, to the upper part of the circle and for negative bias, to the bottom one. Increase of the dimension cause that we can simply draw the line to separate points of different neuron responses. This straight line passes through the center of coordinate system and its gradient depends on w₀ (bias weight). So, bias causes move of the result to the “additional dimension”, and makes solution of some problem possible to solve.

    ::Two dimensional case::

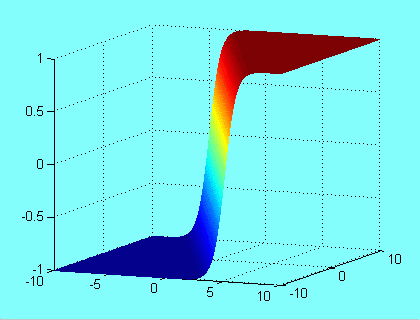
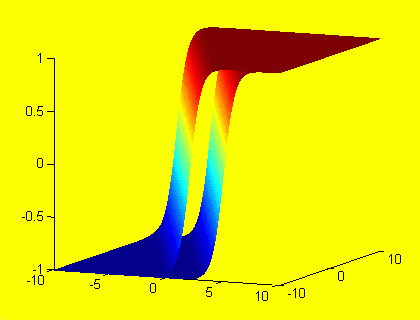
      Now lets see the case of two-dimensional neuron. In the geometrical interpretation all input vectors are in the OXY plane and the neuron output is the third dimension. So the activation function is a surface in the 3 dimensional space, the example of the sigmoidal function is shown in the figure below.

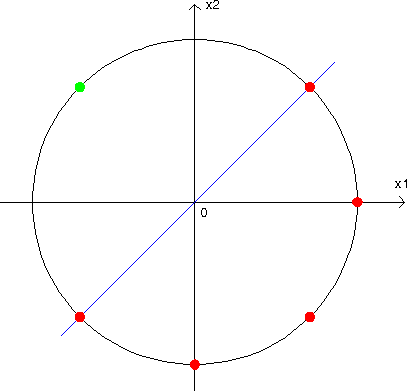
Normalization of the input vectors causes that all of them are moved to the edge of a unitary radius circle, with one exception of point (0,0), which stay on its place. Now we might think about how the bias works in the dual input neuron. At first lets take a look to the activation function only. As we know from the previous chapter, bias input is responsible for moving of activation function toward the straight line. In the two dimensional case bias moves the activate function towards the direction that is perpendicular to the line given by the equation:

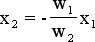
Examples of activation function for neuron with and without a bias are shown in the figure below.

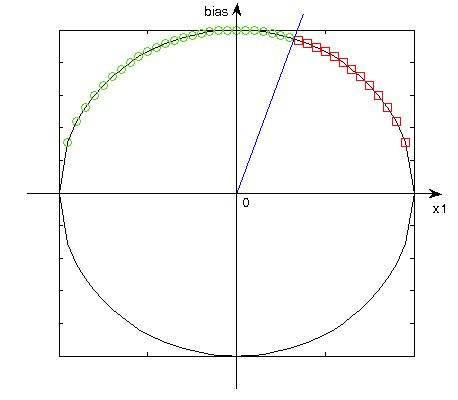
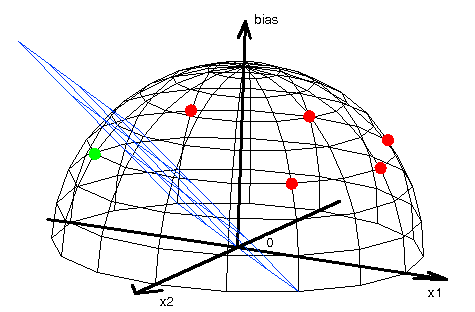
Taking into account neuron with bias addition of an extra weight cause move of input vectors from the two to the three dimensional space. All of points are situated on the sphere; however for the positive bias on top half of sphere, and for negative bias on a bottom sphere part. This is result of the input vectors normalization, namely the third coordinate is constant and that causes points separation for negative and positive bias. The (0,0) point changes to (0,0,1) “the highest” point of sphere or to (0,0,-1), “the lowest” point of sphere.
           Use of bias is necessary to reach any result in some cases. Example of the solution of the one problem using biased and non-biased neuron is shown below.

In these figures we can see that the points are chosen in such a way that for non biased neuron we cannot drive straight line through the center of coordinate system that separates different values of neuron response. Neuron responses for each point was marked by circles colored dependently on the neuron response value. Conclusion is that the non-biased neuron cannot make correct classification of the selected points, so the neuron cannot be leart it. However for the biased neuron the points are moved to the edge of a sphere and because of that they might be separated by plane that passes through the center of coordinates system. Conclusion is that the biased neuron can separate these points.

    ::Summary::

     Use of additional input, which is called bias, of neuron improves properties of the neuron. It allows moving the threshold of activation function. Use of bias increases calculations, because the additional weight have to be determined. That was presented for one and two-dimensional neurons. In the event of neurons with more inputs the situation is similar, however drawing geometrical interpretation of activation function and results of normalizatios would be impossible. For example let's consider 4-input neuron. Normalization of input vectors would be equal to move these points to the sphere in 4 dimensions, which is not possible to illustration. The only way to present this problem would be a 3D animation.