::Wstep teoretyczny::
Podstawowym elementem składowym sieci neuronowej jest neuron. Główną cechą pojedynczego neuronu jest to, że posiada on wiele wejść
i tylko jedno wyjście. Z matematycznego punktu widzenia neuron przedstawia
się jako element realizujący funkcję daną wzorem:
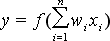
gdzie f() jest funkcją aktywacji, wi wagi dla poszczególnych wejść, xi wartości wejściowe neuronu. Neuron sumuje składowe wektora wejściowego przemnożone przez odpowiednie wagi, a następnie wynik sumowania poddaje działaniu funkcji aktywacji i w ten sposób generowane jest wyjście neuronu. Wektory wejściowe jak i wagi neuronu w rzeczywistych zastosowaniach podlegają często operacji normowania. W interpretacji geometrycznej odpowiada to przeniesieniu punktów wektora wejściowego na powierzchnię N wymiarowej sfery o promieniu jednostkowym, gdzie N jest rozmiarem wektora wejściowego. W najprostszym przypadku, dla wektora dwuwymiarowego, operacji normowania odpowiada przeniesienie wszystkich punktów wejściowych na okrąg o promieniu równym 1. Operacje normowania każdej współrzędnej można zapisać matematycznie za pomocą wzoru:
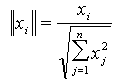
gdzie xi współrzędna normowana, xj kolejne współrzędne wektora wejściowego. Stosowanie operacji normowania zarówno do wektorów wejściowych, jak i wag dla poszczególnych wejść neuronów w znacznym stopniu poprawia właściwości uczonenia neuronu. Rolę funkcji aktywacji może pełnić funkcja liniowa bądź nieliniowa. W przypadku liniowego neuronu jego zapis matematyczny przedstawia się następująco:
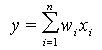
Jest to jeden z najprostszych modeli neuronu rzadko stosowany w praktyce. Wynika to z tego, że zjawiska w otaczającym świecie mają charakter nieliniowy. Można by tu wziąć za przykład biologiczne neurony. Neuron może być wyposażony w tak zwany „bias”, czyli dodatkowe wejście, na którym występuje stała wartość. Waga dla tego wejścia jest modyfikowana w trakcie procesu uczenia tak jak wszystkie pozostałe wagi. Najczęściej przyjmuje się, że na wejściu bias występuje sygnał stale równy jeden, wtedy wzór matematyczny takiego neuronu przedstawia się w sposób następujący:
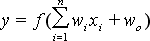
gdzie f() jest funkcją aktywacji, wi wagi dla poszczególnych wejść, xi wartości wejściowe neuronu
natomiast w0 wartość wagi dla wejścia bias. Jeżeli przyjmiemy wartość na wejściu bias równą 0 to otrzymujemy
wzór matematyczny dla zwykłego neuronu.
Teraz zajmiemy się tym do czego owy bias służy.
::Przypadek jednowymiarowy::
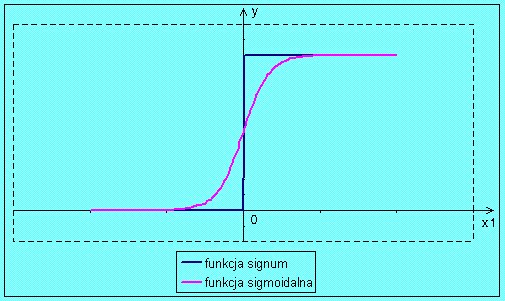
Najprościej działanie biasu można wyjaśnić na podstawie interpretacji geometrycznej dla neuronu o pojedynczym wejściu, dla dwóch wybranych funkcji aktywacji. Tę interpretację
dla funkcji signum i sigmoidalnej przedstawiono na rysunku poniżej.
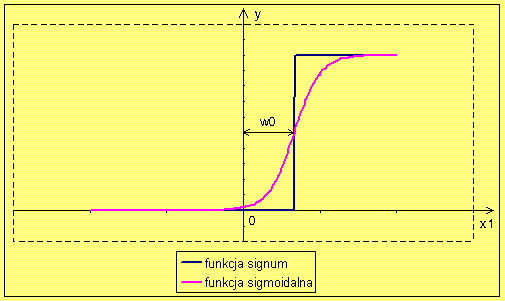
Z wykresów wynika, że w przypadku neuronu jednowejściowego zastosowanie biasu 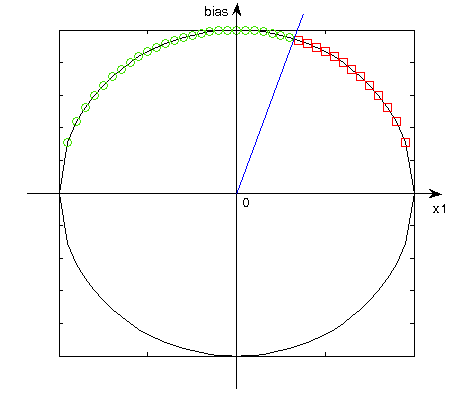 umożliwia przesuwanie progu aktywacji wzdłuż osi x.
Gdy bias jest ujemny przesuwamy próg aktywacji w prawo, gdy dodatni to w lewo. Stąd prosty wniosek, że neuron z biasem
powinien uczyć się nawet takich wektorów których zwykły neuron nie byłby w stanie się nauczyć. Dochodzimy do wniosku, że
dodanie dodatkowej wagi kosztem zwiększenia ilości koniecznych obliczeń powoduje poprawę własności neuronu.
Operacja normowania neuronu jednowejściowego nie ma sensu, gdyż każdy podstawiony punkt po unormowaniu może otrzymać trzy
wartości –1, 0 lub 1.
umożliwia przesuwanie progu aktywacji wzdłuż osi x.
Gdy bias jest ujemny przesuwamy próg aktywacji w prawo, gdy dodatni to w lewo. Stąd prosty wniosek, że neuron z biasem
powinien uczyć się nawet takich wektorów których zwykły neuron nie byłby w stanie się nauczyć. Dochodzimy do wniosku, że
dodanie dodatkowej wagi kosztem zwiększenia ilości koniecznych obliczeń powoduje poprawę własności neuronu.
Operacja normowania neuronu jednowejściowego nie ma sensu, gdyż każdy podstawiony punkt po unormowaniu może otrzymać trzy
wartości –1, 0 lub 1.
Przyjrzyjmy się więc operacji normowania dla jednowymiarowego neuronu z biasem.
Wykonywanie tej operacji na wektorach wejściowych (przyjmujemy bias jako wejście o wartości 1) i wagach neuronu powoduje przeniesienie
wszystkich punktów na okrąg o promieniu równym 1. Wynik takiej operacji przedstawiono obok.
Operacja normalizacji powoduje, w zależności od znaku biasu, przeniesienie wszystkich punktów na odpowiednią część okręgu.
W przypadku dodatniego biasu na górną część okręgu, natomiast w przypadku ujemnego biasu na dolną. Zwiększenie wymiaru
powoduje to, że w łatwy sposób można przeprowadzić linię rozgraniczającą od siebie punkty o różnych odpowiedziach neuronu.
Ta linia prosta przechodzić będzie przez środek układu współrzędnych, jej nachylenie zależeć będzie od w0 (waga dla biasu).
Czyli bias powoduje przeniesienie rozwiązania w „dodatkowy wymiar”, przez co rozwiązanie danego problemu staje się w ogóle
możliwe.
::Przypadek dwuwymiarowy::
Przyjrzyjmy się teraz neuronowi dwuwejściowemu. W interpretacji geometrycznej wektory wejściowe
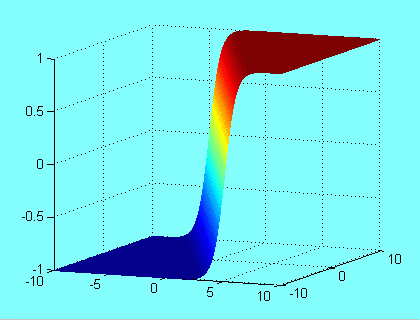
należą do całej płaszczyzny OXY, natomiast wyjście neuronu stanowi trzeci wymiar. Czyli funkcja aktywacji jest pewną powierzchnią w przestrzeni trójwymiarowej, przykład funkcji sigmoidalnej
przedstawiono obok.
Operacja normowania wektorów wejściowych sprawia, że wszystkie punkty przenoszone są na obwód okręgu o promieniu 1, wyjątkiem jest oczywiście punkt (0,0) który operacja normowania przekształca w ten sam punkt. Teraz należy zastanowić się jak bias wpływa na działanie neuronu dwuwejściowego. Przyjrzyjmy się najpierw samej funkcji aktywacji. Jak już wiemy z poprzedniego punktu wejście biasu jest odpowiedzialne za przesuwanie funkcji aktywacji wzdłuż linii prostej. W przypadku dwuwymiarowym bias przesuwa funkcję aktywacji w kierunku prostopadłym do prostej o równaniu:
rys 3. Funkcja aktywacji dla neuronu dwu wejściowego.
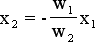
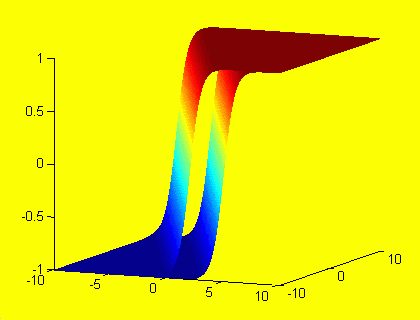
Przykłady funkcji aktywacji przesuniętej i nie przesuniętej w wyniku działania biasu przedstawiono obok.
Rozważając neuron z biasem wprowadzenie dodatkowej wagi powoduje
przeniesienie wektorów wejściowych z przestrzeni dwu do trójwymiarowej. Wszystkie punkty leżą wtedy na powierzchni
sfery, z tym, że dla dodatniej wartości biasu jest to górna, a dla ujemnej dolna półsfera. Wynika to w prosty sposób
z metody obliczania normy dla wektorów wejściowych, mianowicie trzecia współrzędna jest przez cały czas stała, co
powoduje rozgraniczenie punktów dla dodatniej i ujemnej wartości biasu. Punkt (0,0) przenosi się w tym przypadku na
punkt (0,0,1) czyli na „najwyżej” położny punkt sfery lub też na punkt (0,0,-1) czyli punkt położony „najniżej”.
rys 4. Obrazy funkcji aktywacji dla neuronu z biasem i bez biasu.
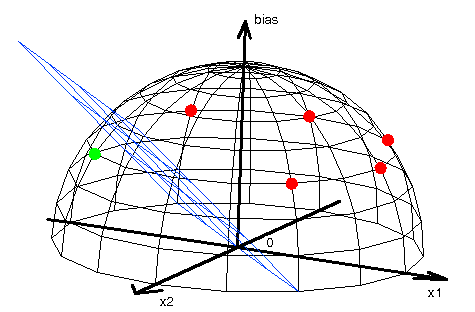
Zastosowanie biasu jest czasami konieczne do uzyskania jakiegokolwiek rozwiązania. Przykład rozwiązania tego samego problemu z wykorzystaniem neuronu z i bez biasu przedstawiono poniżej.
Z rysunków wynika rzecz następująca, w przypadku neuronu bez biasu punkty zostały dobrane tak, aby nie dało się przeprowadzić prostej, przechodzącej przez środek układu współrzędnych rozdzielającej punkty o różnych wartościach odpowiedzi neuronu. Odpowiedzi neuronu dla danego punktu zaznaczone są kółkami w odpowiednich kolorach zależnych od wartości tej odpowiedzi. Wniosek jest następujący neuron bez biasu nie jest w stanie prawidłowo zaklasyfikować punktów, czyli nie jesteśmy w stanie go tego nauczyć. Natomiast w przypadku neuronu z biasem przeniesienie punktów na powierzchnie sfery umożliwia rozgraniczenie punktów o różnych wartościach na wyjściu neuronu za pomocą płaszczyzny przechodzącej przez środek układu. Wynika z tego, że neuron jest w stanie nauczyć się rozróżniać dane punkty.
::Wnioski::
Wprowadzenie do neuronu dodatkowego wejścia bias
powoduje wzrost ich możliwości uczenia się. Jest to związane z umożliwianiem przesuwania progu aktywacji w zależności
od wagi biasu. Zastosowanie biasu powoduje jednak wzrost ilości obliczeń wynikający z konieczności ustalania dodatkowej
wagi. Tak dzieje się dla neuronów jedno i dwuwejściowych. W przypadkach neuronów z większą ilością wejść będzie bardzo
podobnie, jednakże przedstawienie geometryczne funkcji aktywacji czy też wyników operacji normowania było by niemożliwe.
Weźmy za przykład neuron 4 wejściowy. Operacja normowania wektorów wejściowych wiązała by się z przeniesieniem ich na
sferę w czterech wymiarach czego nie da się przedstawić za pomocą płaskiego rysunku. Jedyną możliwością przedstawienia
takiego zagadnienia, była by 3D animacja.
Literatura:
Ryszard Tadeusiewcz "Sieci neuronowe", Kraków 1992
Andrzej Kos, Wykład "Sieci neuronowe i sztuczna inteligencja w elektronice", 2004/2005
Krzysztof Ziaja, Piotr Miernikowski
Katedra Elektroniki AGH