Ćwiczenie 3

Identyfikacja obiektów regulacji

Cel i zakres ćwiczenia

Celem ćwiczenia jest zaznajomienie się z przykładami parametrycznej identyfikacji obiektów dynamicznych.

Dla potrzeb regulacji automatycznej, zwykle wystarczy uproszczony model rzeczywistego obiektu - zadany w postaci transmitancji operatorowej. Zakładając w sposób arbitralny postać modelu, sprowadzamy zagadnienie identyfikacji obiektu do wyznaczenia najlepszych, w określonym sensie, parametrów tego modelu. Zastosowana metoda identyfikacji bazuje na charakterystyce skokowej zdjętej na badanym obiekcie.

Przyjmiemy następujące modele transmitancyjne obiektów:

1. Inercyjny I- ego rzędu z opóźnieniem

2. Inercyjny II- ego rzędu z opóźnieniem

3. Oscylacyjny II- ego rzędu

4. Inercyjny n- tego rzędu

Wykonanie ćwiczenia

Wyznaczanie parametrów modelu obiektu należy przeprowadzić w następujący sposób:

- załadować do przestrzeni roboczej Matlab-a wyniki pomiarów charakterystyki skokowej zdjętej na obiekcie, poleceniem load pomiary (plik o nazwie pomiary pobrać tutaj),

- sporządzić wykres charakterystyki skokowej (można użyć sekwencji poleceń: load pomiary; k = length(pomiary); t = linspace(0, 300, k); plot(t, pomiary);),

- obliczyć wzmocnienie obiektu oraz opóźnienie T_o, i stałą czasową T (dwiema metodami; Zieglera – Nicholsa i Braid’a),

- wykonać charakterystyki skokowe modelu dla tak wyznaczonych parametrów, dla porównania zamieścić wspólnie z charakterystyką pomierzoną.

W drugiej części ćwiczenia należy wyznaczyć parametry dla podanych modeli posiłkując się metodą najmniejszych kwadratów. W tym celu przyjmujemy z grubsza oszacowane wartości parametrów. Z kolei wyznaczamy odpowiedź modelu dla przyjętych wartości parametrów, a następnie sprawdzamy na ile jest ona zgodna z przebiegiem doświadczalnym uzyskanym na obiekcie rzeczywistym. Jako kryterium zgodności przyjmujemy odchylenie średniokwadratowe:

gdzie m – liczba wyników pomiarowych, x_i – i-ty wynik pomiaru, y(t_i) – wartość wynikająca z aproksymacji.

Proces doboru parametrów należy kontynuować aż do uzyskania minimum wartości kryterium odchylenia średniokwadratowego J.

Uwaga! W pewnych przypadkach identyfikacja obiektu jest możliwa wyłącznie w warunkach ruchowych, wtedy również wejście (sterowanie) podlega zakłóceniom. W tych sytuacjach do identyfikacji obiektu stosuje się nowoczesne metody oparte o zasadę najmniejszych kwadratów i teorię estymacji oraz metody błędu predykcji. Metody te zostały zaimplementowane w Matlab–ie i można je znaleźć w bibliotece Identification Toolbox pod takimi nazwami, jak np. ar (Auto Regressive), bj (Boxa-Jenkinsa) i inne.

Przykład 1

Przykład wykonania aproksymacji metodą najmniejszych kwadratów, zrealizowano w postaci listy poleceń Matlab–a, zamieszczonej w m-pliku o nazwie cw3.m.

Zbiór danych doświadczalnych, zapisany na plik w postaci binarnej pod nazwą pomiary, ładowany jest do przestrzeni roboczej Matlab–a, za pomocą polecenia load pomiary. W celu urealnienia zagadnienia identyfikacji do sygnału pomierzonej odpowiedzi obiektu, dodano zakłócenie o charakterze procesu stochastycznego o rozkładzie normalnym.

Poniżej przedstawiono przykładowy wynik wykonania aproksymacji Strejca metodą najmniejszych kwadratów.

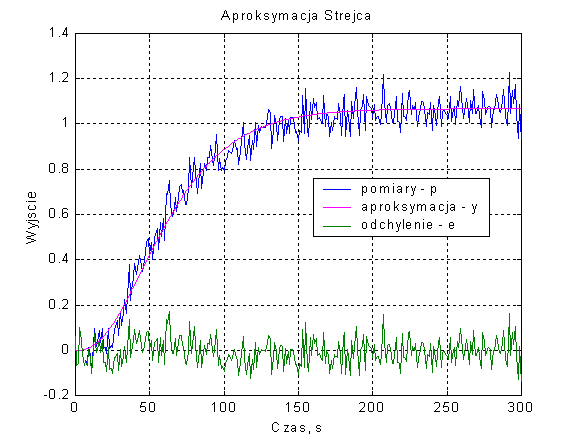
Rys. 1. Aproksymacja Strejca trzeciego rzędu