---

Koncepcje i Modele Programowania

---

Programowanie z ograniczeniami

Wprowadzenie

1. Programowanie ograniczeniowe (constraint programming) służy do rozwiązywania problemów zgodności z ograniczeniami (Constraint Satisfaction Problem, CSP).
2. Zbliża się do idealnego programowania deklaratywnego: specyfikujemy co chcemy zrobić nie precyzująć jak.

Przeszukiwanie z propagacją informacji

1. Na tę technikę składają się trzy zasady:
   1. Gromadzenie informacji cząstkowych - np. w każdym rozwiązaniu X jest mniejsze niż 100
   2. Lokalna dedukcja - z dwóch lub kilku informacji dedukujemy kolejne, np. jeśli X>100 i Y>X to Y>=101
   3. Kontrolowane przeszukiwanie - gdy już nie można przeprowadzić lokalnych dedukcji, dokonujemy przeszukiwania wg zasady podziału problemu P na dwa rozłączne podproblemy: P^C oraz P^¬C, gdzie C jest pewnym nowym ograniczeniem. Wybór C ma kluczowe znaczenie.

2. Podstawowe pojęcia: propagatory i ograniczenia podstawowe
   • Ograniczenia podstawowe - reprezentowane bezpośrednio w obszarze jednokrotnego przypisania, postaci X=Y lub wyrażające przynależność do jakiejś domeny. Przykłady:

     X=osoba(wiek:Y)
     X::5#10
     

   • Propagator - wątek, którego zadaniem jest ciągłe kontrolowanie zawartości obszaru i dodawanie do niego ograniczeń podstawowych. Gdy zmieni się domena jakiejś zmiennej, propagator, który ją wykorzystuje wykonuje swój kod w celu dostarczenia (propagacji) nowej informacji cząstkowej. Przykłady ograniczeń, które są propagatorami:

     X*Y=:24
     X+Y=:10
     X=<:Y
     

3. Przykład drzewa poszukiwań

   Początkowe ograniczenia:

   X<>7 Z<>2 X-Z=3*Y
   X należy do zbioru {1, 2, ... 8}
   Y należy do zbioru {1, 2, ... 10}
   Z należy do zbioru {1, 2, ... 10}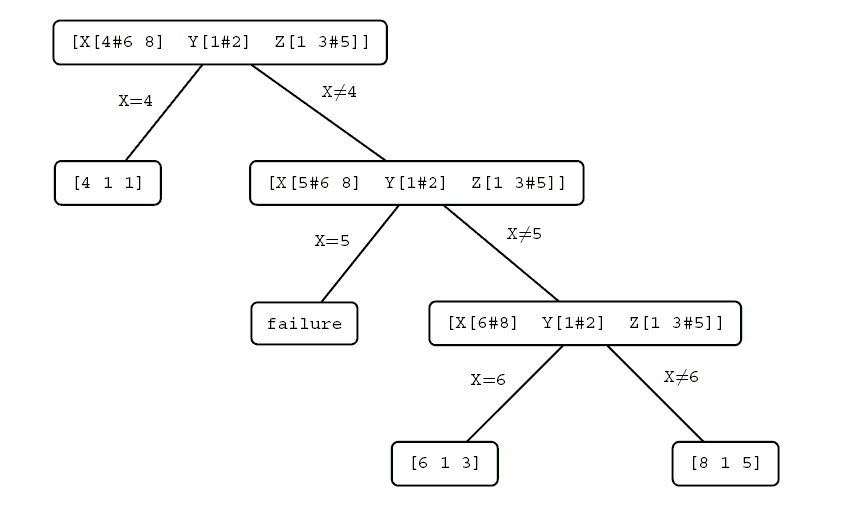
   

   
4. Definicja ograniczeń
   • X::90#110 - X należy do zbioru {90, 91, ... , 110}
   • Równość i nierówność: =: <: >: =<: =>: \=:
   • {FD.distinct Xs} - tworzy propagator narzucający na zbiór Xs wymaganie, by jego elementy były parami różne. Xs może być rekordem lub listą zmiennych należących do domen skończonych.
   • {FD.distance X Y '=:' Z} - tworzy propagator narzucający wymaganie, by "odległość" między zmiennymi X i Y była równa Z, tzn. |X-Y|=Z. Zamiast równości dopuszczalne są inne operatory.
   • Inne propagatory

5. Przykład: czy istnieje prostokąt o powierzchni 24 jednostek kwadratowych i obwodze 20 jednostek?. Z warunków tego zadania wynikają następujące ograniczenia:
   • X*Y=:24
   • X+Y=:10
   • X=<:Y (możemy tak założyć)
   • X::1#9 (ze względu na sumę X+Y)
   • X::1#9 (j.w.)
6. W oz:

   proc {Rectangle ?Sol}
     sol(X Y)=Sol
   in
     X::1#9 Y::1#9
     X*Y=:24 X+Y=:10 X=<:Y
     {FD.distribute naive Sol}
   end
   
   {Browse {SearchAll Rectangle}}
   

7. FD.distribute - wybór strategii podziału problemu. Strategia naive oznacza, że wybierana jest pierwsza niezdeterminowana zmienna krotki Sol i jako kryterium podziału przyjmowana jest najmniejsza wartość z jej domeny. Np. jeśli w wyniku lokalnych dedukcji dojdziemy do ograniczeń:

   X=4
   Y::5#6
   

   to zmienna X jest zdeterminowana, zaś zmienna Y nie jest i jako warunek podziału przyjmowane jest Y=5.

8. Przykład: Kryptarytmy

   Przykładowy kryptarytm:

     S E N D
   + M O R E
   ---------
   M O N E Y
   

   Każda litera reprezentuje jakąś cyfrę, przy czym różne litery oznaczają różne cyfry. Liczby nie zaczynają się od zera. Należy znaleźć przyporządkowanie cyfr literom spełniajace podaną zależność.

9. Rozwiązanie tego przykładu:

   proc {SendMoreMoney ?Sol}
     S E N D M O R Y
   in
     Sol=sol(s:S e:E n:N d:D m:M o:O r:R y:Y) 
     Sol:::0#9 
     {FD.distinct Sol} 
     S\=:0 
     M\=:0
     1000*S + 100*E + 10*N + D 
     + 1000*M + 100*O + 10*R + E
     =: 10000*M + 1000*O + 100*N + 10*E + Y
     {FD.distribute ff Sol} 
   end
   

   W tym wypadku zastosowana jest strategia podziału ff, czyli first-fail. W tym przypadku najpierw wybierana jest zmienna o najmniejszej liczbie możliwości i dla niej wybierana jest najmniejsza wartość.

   Operator ::: oznacza, że ograniczenie (przynależności do zbioru) ma dotyczyć każdego elementu struktury.

---

Bartosz Baliś, balis at uci.agh.edu.pl
Maciej Malawski, malawski at uci.agh.edu.pl

---